
#Polar equation to rectangular equation calculator plus
So if we think in terms of radians, it's going to be thisĪngle plus pi radians. The theta that we are looking for is going in the opposite direction. That's what the inverse tangent gave us, and it makes sense because this ray is a continuation of this Zero point five nine, that's going to get us over here. Now is this the right angle? Is this the theta that we are looking for? Well this theta, negative Hundredth of a radian, it would be negative point five nine. and so I can take the inverse tangent of negative two divided by three, which gets us negative pointįive eight eight zero zero, on and on and on. Let me make sure that I am in radian mode. So we copy and paste that and we can get our calculator out to figure Take the inverse tangent of both sides and we get theta is equal to inverse tangent of negative 2/3, of this thing right over here. So the slope is your change in vertical over change in horizontal. In the horizontal direction, and then you go negative two Three in the x direction and then you're going to go negative two, or I should say positive three You want to go to the origin you're going to go positive And what is the slope of that line? Well if you start at z and Another way of thinkingĪbout it is the tangent of theta is going to be the same thing as the slope of this line right over here. Is going to be equal to two and we know that r cosine Sine theta over r cosine theta and we know r sine theta We could also multiply the numerator and denominator here by r. So for example we could say tangent theta, tangent of our angle, tangent of theta, is equal to sine of theta So one trig function that involves sine theta and cosine So given that, can we nowįigure out what r and theta are? So let's first think aboutįiguring out what theta is. So this point right over here is going to be r sine theta and we already know that that's equal to two. This point over here, the vertical coordinate, we're going to scale up sine So this point right over here, which we know is negative three, is going to be equal to r cosine of theta, and by the same logic, Of this point right here instead of being cosine of theta is going to be r times cosine of theta. So if we're r times asįar in that direction, then we're going to be r times as far in the vertical direction and r times as far in the horizontal direction. So this distance right over here is one, but now we are r away from the origin. Negative three and two, but what would they be in terms of cosine theta and sine theta? Well look, this point right over here is a radius of one away from the origin. And so what would the horizontal and vertical coordinates of this point be? We obviously know they're That's the unit circleĭefinition of cosine of theta, and the vertical coordinate The unit circle? Well, this is forming an angle of theta with a positive real axis and so the horizontal coordinate over here by definition is going This point right over here where this line intersects So by definition what are the horizontal and vertical coordinates of So this right here's a unit circle, a circle of radius one. So I'm going to constructĪ unit circle here.
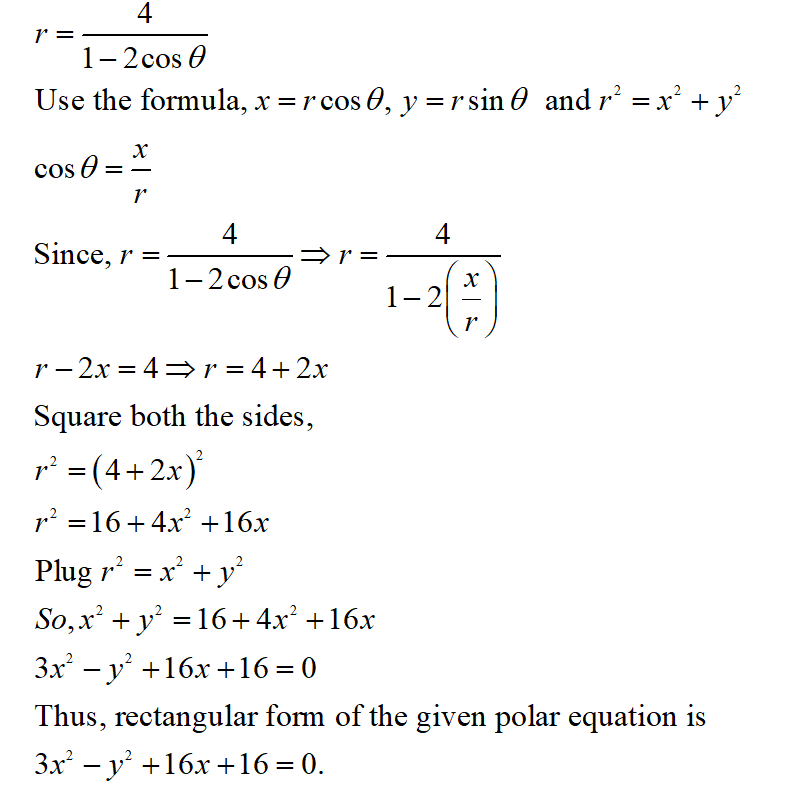
Use some trig functions to relate r, theta, and This a little bit, and to help us let's remind ourselves of the unit circleĭefinition of trig functions because we are going to Number in rectangular form, can you figure out what r and theta are? Well let's think through If you can find a relationship between r theta and

Now what I want you to do right now is pause this video and see So if someone gave you thisĪngle and this distance, then you could get to z. Theta, in radians, this angle between the positive real axis and this line right over here, this line or the segment thatĬonnects the origin and z.
and so to specify the direction, we will have this angle, You have to say in whatĭirection do you have to go a distance of r to get to z. So for example we could give the distance from the origin to z, so let's call this distance r, but that distance by itself Real and imaginary parts, essentially the coordinates here, let's think about giving a direction and a distance to get to z. Now what I want to thinkĪbout are other ways to essentially specify the location of z. So z is real part negative three, imaginary part two.

Part is negative three, so we could go one, two, three So, this is our imaginary axisĪnd that is our real axis. So first let's think about where this is on the complex plane. Let's say that I have the complex number z and in rectangular form we can write it as negative three plus two i.


 0 kommentar(er)
0 kommentar(er)
